บทความนี้ได้รวบรวม ตารางของไซน์ โคไซน์ แทนเจนต์และโคแทนเจนต์. ก่อนอื่นเราให้ตารางค่าพื้นฐานของฟังก์ชันตรีโกณมิตินั่นคือตารางไซน์โคไซน์แทนเจนต์และโคแทนเจนต์ของมุม 0, 30, 45, 60, 90, ..., 360 องศา ( 0, π/6, π/4, π/3, π/2, …, 2πเรเดียน). หลังจากนั้นเราจะให้ตารางไซน์และโคไซน์รวมถึงตารางแทนเจนต์และโคแทนเจนต์โดย V. M. Bradis และแสดงวิธีใช้ตารางเหล่านี้เมื่อค้นหาค่าของฟังก์ชันตรีโกณมิติ

การนำทางหน้า

ตารางของไซน์ โคไซน์ แทนเจนต์และโคแทนเจนต์สำหรับมุม 0, 30, 45, 60, 90, ... องศา

บรรณานุกรม.

• พีชคณิต: Proc. สำหรับ 9 เซลล์ เฉลี่ย โรงเรียน / ยู. N. Makarychev, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova; เอ็ด S. A. Telyakovsky.- M.: การตรัสรู้, 1990.- 272 p.: Ill.- ISBN 5-09-002727-7
• Bashmakov M.I.พีชคณิตและจุดเริ่มต้นของการวิเคราะห์: Proc. สำหรับ 10-11 เซลล์ เฉลี่ย โรงเรียน - ครั้งที่ 3 - ม.: ตรัสรู้, 2536. - 351 น.: ป่วย. - ไอเอสบีเอ็น 5-09-004617-4
• พีชคณิตและจุดเริ่มต้นของการวิเคราะห์: Proc. สำหรับ 10-11 เซลล์ การศึกษาทั่วไป สถาบัน / A. N. Kolmogorov, A. M. Abramov, Yu. P. Dudnitsyn และคนอื่น ๆ ; เอ็ด A. N. Kolmogorova.- 14th ed.- M.: การตรัสรู้, 2004.- 384 p.: Ill.- ISBN 5-09-013651-3
• Gusev V. A. , Mordkovich A. G.คณิตศาสตร์ (คู่มือสำหรับผู้สมัครเข้าโรงเรียนเทคนิค): Proc. เบี้ยเลี้ยง.- ม.; สูงกว่า ร.ร. 2527-351 น.
• แบรดดิส วี.เอ็ม.ตารางคณิตศาสตร์สี่หลัก: สำหรับการศึกษาทั่วไป หนังสือเรียน สถานประกอบการ - ครั้งที่ 2 - M.: Bustard, 1999.- 96 p.: ill. ISBN 5-7107-2667-2

ตารางค่าของ sines (sin), cosines (cos), tangents (tg), cotangents (ctg) เป็นเครื่องมือที่ทรงพลังและมีประโยชน์ที่ช่วยแก้ปัญหามากมายทั้งทางทฤษฎีและทางประยุกต์ ในบทความนี้ เราจะจัดเตรียมตารางฟังก์ชันตรีโกณมิติพื้นฐาน (ไซน์ โคไซน์ แทนเจนต์ และโคแทนเจนต์) สำหรับมุม 0, 30, 45, 60, 90, ..., 360 องศา (0, π 6 , π 3 , π 2 , . . . , 2 π เรเดียน). ตาราง Bradis แยกสำหรับไซน์และโคไซน์ แทนเจนต์ และโคแทนเจนต์จะแสดงพร้อมคำอธิบายวิธีใช้เพื่อค้นหาค่าของฟังก์ชันตรีโกณมิติพื้นฐาน

ตารางฟังก์ชันตรีโกณมิติพื้นฐานสำหรับมุม 0, 30, 45, 60, 90, ..., 360 องศา

ตามคำจำกัดความของไซน์ โคไซน์ แทนเจนต์ และโคแทนเจนต์ คุณสามารถค้นหาค่าของฟังก์ชันเหล่านี้สำหรับมุม 0 และ 90 องศา

บาป 0 = 0 , cos 0 = 1 , t g 0 = 0 , โคแทนเจนต์ของศูนย์ - ไม่ได้กำหนดไว้

sin 90 ° = 1 , cos 90 ° = 0 , โดยที่ t g 90 ° = 0 , ไม่ได้กำหนดแทนเจนต์เก้าสิบองศา

ค่าของไซน์ โคไซน์ แทนเจนต์และโคแทนเจนต์ในเส้นทางเรขาคณิตถูกกำหนดให้เป็นอัตราส่วนของด้านข้างของสามเหลี่ยมมุมฉากซึ่งมีมุม 30, 60 และ 90 องศาและ 45, 45 และ 90 องศา .

นิยามของฟังก์ชันตรีโกณมิติสำหรับมุมแหลมในรูปสามเหลี่ยมมุมฉาก

ไซนัสคืออัตราส่วนของขาตรงข้ามกับด้านตรงข้ามมุมฉาก

โคไซน์คืออัตราส่วนของขาที่อยู่ติดกันต่อด้านตรงข้ามมุมฉาก

แทนเจนต์- อัตราส่วนของขาตรงข้ามกับขาที่อยู่ติดกัน

โคแทนเจนต์- อัตราส่วนของขาที่อยู่ติดกันกับด้านตรงข้าม

ตามคำจำกัดความจะพบค่าของฟังก์ชัน:

บาป 30 ° = 1 2 , cos 30 ° = 3 2 , t g 30 ° = 3 3 , c t g 30 ° = 3 , บาป 45 ° = 2 2 , cos 45 ° = 2 2 , t g 45 ° = 1 , c t g 45 ° = 1 , บาป 60 ° = 3 2 , cos 45 ° = 1 2 , t g 45 ° = 3 , c t g 45 ° = 3 3

มาสรุปค่าเหล่านี้ในตารางและเรียกมันว่าตารางค่าพื้นฐานของไซน์ โคไซน์ แทนเจนต์ และโคแทนเจนต์

ตารางค่าพื้นฐานของไซน์ โคไซน์ แทนเจนต์และโคแทนเจนต์

α °	0	30	45	60	90
บาป	0	1 2	2 2	3 2	1
cosα	1	3 2	2 2	1 2	0
tgα	0	3 3	1	3	ไม่ได้กำหนด
c t g	ไม่ได้กำหนด	3	1	3 3	0
α , r a d ฉัน n	0	พาย6	π 4	π 3	π 2

คุณสมบัติที่สำคัญอย่างหนึ่งของฟังก์ชันตรีโกณมิติคือคาบ ตามคุณสมบัตินี้ ตารางนี้สามารถขยายได้โดยใช้สูตรการแคสต์ ด้านล่างเรานำเสนอตารางค่าของฟังก์ชันตรีโกณมิติหลักสำหรับมุม 0, 30, 60, ..., 120, 135, 150, 180, ..., 360 องศา (0, π 6, π 3, π 2, . . . , 2 pi เรเดียน).

ตารางของไซน์ โคไซน์ แทนเจนต์และโคแทนเจนต์

α °	0	30	45	60	90	120	135	150	180	210	225	240	270	300	315	330	360
บาป	0	1 2	2 2	3 2	1	3 2	2 2	1 2	0	- 1 2	- 2 2	- 3 2	- 1	- 3 2	- 2 2	- 1 2	0
cosα	1	3 2	2 2	1 2	0	- 1 2	- 2 2	- 3 2	- 1	- 3 2	- 2 2	- 1 2	0	1 2	2 2	3 2	1
tgα	0	3 3	1	3	-	- 1	- 3 3	0	0	3 3	1	3	-	- 3	- 1		0
c t g	-	3	1	3 3	0	- 3 3	- 1	- 3	-	3	1	3 3	0	- 3 3	- 1	- 3	-
α , r a d ฉัน n	0	พาย6	π 4	π 3	π 2	2 ปี 3	3 π 4	5 ปี่ 6	π	7 ปี่ 6	5 ปี 4	4 ปี 3	3 ปี 2	5 ปี 3	7 ปี 4	11 ปี่ 6	2 ปี่

ความเป็นคาบของไซน์ โคไซน์ แทนเจนต์ และโคแทนเจนต์ ช่วยให้คุณขยายตารางนี้เป็นมุมขนาดใหญ่ได้ตามอำเภอใจ ค่าที่รวบรวมไว้ในตารางมักใช้ในการแก้ปัญหา ดังนั้นจึงแนะนำให้เรียนรู้ด้วยใจ

วิธีใช้ตารางค่าพื้นฐานของฟังก์ชันตรีโกณมิติ

หลักการใช้ตารางค่าของไซน์ โคไซน์ แทนเจนต์และโคแทนเจนต์มีความชัดเจนในระดับที่เข้าใจง่าย จุดตัดของแถวและคอลัมน์ให้ค่าฟังก์ชันสำหรับมุมใดมุมหนึ่ง

ตัวอย่าง. วิธีใช้ตารางไซน์ โคไซน์ แทนเจนต์ และโคแทนเจนต์

คุณต้องค้นหาว่าบาป 7 π 6 เท่ากับ .อะไร

เราพบคอลัมน์ในตาราง ค่าของเซลล์สุดท้ายซึ่งเท่ากับ 7 π 6 เรเดียน - เท่ากับ 210 องศา จากนั้นเราเลือกเงื่อนไขของตารางที่แสดงค่าของไซน์ ที่จุดตัดของแถวและคอลัมน์ เราพบค่าที่ต้องการ:

บาป 7 π 6 \u003d - 1 2

โต๊ะ Bradis

ตาราง Bradis ช่วยให้คุณคำนวณค่าของไซน์ โคไซน์ แทนเจนต์ หรือโคแทนเจนต์ได้อย่างแม่นยำถึงทศนิยม 4 ตำแหน่งโดยไม่ต้องใช้เทคโนโลยีคอมพิวเตอร์ นี่เป็นการทดแทนเครื่องคิดเลขทางวิศวกรรมชนิดหนึ่ง

อ้างอิง

Vladimir Modestovich Bradis (1890 - 1975) - นักคณิตศาสตร์และครูโซเวียตตั้งแต่ปี 1954 เป็นสมาชิกที่สอดคล้องกันของ APS ของสหภาพโซเวียต ตารางลอการิทึมสี่หลักและปริมาณตรีโกณมิติธรรมชาติ พัฒนาโดย Bradis ปรากฏครั้งแรกในปี 1921

อันดับแรก เราให้ตาราง Bradys สำหรับไซน์และโคไซน์ ช่วยให้คำนวณค่าโดยประมาณของฟังก์ชันเหล่านี้ได้อย่างแม่นยำสำหรับมุมที่มีจำนวนองศาและนาทีเป็นจำนวนเต็ม คอลัมน์ซ้ายสุดของตารางแสดงองศา ขณะที่แถวบนสุดแสดงนาที โปรดทราบว่าค่าทั้งหมดของมุมตารางของ Bradys มีค่าเป็นทวีคูณของหกนาที

ตาราง Bradis สำหรับไซน์และโคไซน์

บาป	0"	6"	12"	18"	24"	30"	36"	42"	48"	54"	60"	cos	1"	2"	3"
											0.0000	90°
0°	0.0000	0017	0035	0052	0070	0087	0105	0122	0140	0157	0175	89°	3	6	9
1°	0175	0192	0209	0227	0244	0262	0279	0297	0314	0332	0349	88°	3	6	9
2°	0349	0366	0384	0401	0419	0436	0454	0471	0488	0506	0523	87°	3	6	9
3°	0523	0541	0558	0576	0593	0610	0628	0645	0663	0680	0698	86°	3	6	9
4°	0698	0715	0732	0750	0767	0785	0802	0819	0837	0854	0.0872	85°	3	6	9
5 °	0.0872	0889	0906	0924	0941	0958	0976	0993	1011	1028	1045	84°	3	6	9
6°	1045	1063	1080	1097	1115	1132	1149	1167	1184	1201	1219	83°	3	6	9
7°	1219	1236	1253	1271	1288	1305	1323	1340	1357	1374	1392	82°	3	6	9
8°	1392	1409	1426	1444	1461	1478	1495	1513	1530	1547	1564	81°	3	6	9
9°	1564	1582	1599	1616	1633	1650	1668	1685	1702	1719	0.1736	80 °	3	6	9
10°	0.1736	1754	1771	1788	1805	1822	1840	1857	1874	1891	1908	79°	3	6	9
11°	1908	1925	1942	1959	1977	1994	2011	2028	2045	2062	2079	78°	3	6	9
12°	2079	2096	2113	2130	2147	2164	2181	2198	2215	2233	2250	77°	3	6	9
13°	2250	2267	2284	2300	2317	2334	2351	2368	2385	2402	2419	76°	3	6	8
14°	2419	2436	2453	2470	2487	2504	2521	2538	2554	2571	0.2588	75°	3	6	8
15°	0.2588	2605	2622	2639	2656	2672	2689	2706	2723	2740	2756	74°	3	6	8
16°	2756	2773	2790	2807	2823	2840	2857	2874	2890	2907	2924	73°	3	6	8
17°	2924	2940	2957	2974	2990	3007	3024	3040	3057	3074	3090	72°	3	6	8
18°	3090	3107	3123	3140	3156	3173	3190	3206	3223	3239	3256	71°	3	6	8
19°	3256	3272	3289	3305	3322	3338	3355	3371	3387	3404	0.3420	70 องศา	3	5	8
20°	0.3420	3437	3453	3469	3486	3502	3518	3535	3551	3567	3584	69°	3	5	8
21°	3584	3600	3616	3633	3649	3665	3681	3697	3714	3730	3746	68°	3	5	8
22°	3746	3762	3778	3795	3811	3827	3843	3859	3875	3891	3907	67°	3	5	8
23°	3907	3923	3939	3955	3971	3987	4003	4019	4035	4051	4067	66°	3	5	8
24°	4067	4083	4099	4115	4131	4147	4163	4179	4195	4210	0.4226	65°	3	5	8
25°	0.4226	4242	4258	4274	4289	4305	4321	4337	4352	4368	4384	64°	3	5	8
26°	4384	4399	4415	4431	4446	4462	4478	4493	4509	4524	4540	63°	3	5	8
27°	4540	4555	4571	4586	4602	4617	4633	4648	4664	4679	4695	62°	3	5	8
28°	4695	4710	4726	4741	4756	4772	4787	4802	4818	4833	4848	61°	3	5	8
29°	4848	4863	4879	4894	4909	4924	4939	4955	4970	4985	0.5000	60°	3	5	8
30°	0.5000	5015	5030	5045	5060	5075	5090	5105	5120	5135	5150	59°	3	5	8
31°	5150	5165	5180	5195	5210	5225	5240	5255	5270	5284	5299	58°	2	5	7
32°	5299	5314	5329	5344	5358	5373	5388	5402	5417	5432	5446	57°	2	5	7
33°	5446	5461	5476	5490	5505	5519	5534	5548	5563	5577	5592	56°	2	5	7
34°	5592	5606	5621	5635	5650	5664	5678	5693	5707	5721	0.5736	55°	2	5	7
35°	0.5736	5750	5764	5779	5793	5807	5821	5835	5850	5864	0.5878	54°	2	5	7
36°	5878	5892	5906	5920	5934	5948	5962	5976	5990	6004	6018	53°	2	5	7
37°	6018	6032	6046	6060	6074	6088	6101	6115	6129	6143	6157	52°	2	5	7
38°	6157	6170	6184	6198	6211	6225	6239	6252	6266	6280	6293	51°	2	5	7
39°	6293	6307	6320	6334	6347	6361	6374	6388	6401	6414	0.6428	50°	2	4	7
40°	0.6428	6441	6455	6468	6481	6494	6508	6521	6534	6547	6561	49°	2	4	7
41°	6561	6574	6587	6600	6613	6626	6639	6652	6665	6678	6691	48°	2	4	7
42°	6691	6704	6717	6730	6743	6756	6769	6782	6794	6807	6820	47°	2	4	6
43°	6820	6833	6845	6858	6871	6884	6896	8909	6921	6934	6947	46°	2	4	6
44°	6947	6959	6972	6984	6997	7009	7022	7034	7046	7059	0.7071	45 °	2	4	6
45 °	0.7071	7083	7096	7108	7120	7133	7145	7157	7169	7181	7193	44°	2	4	6
46°	7193	7206	7218	7230	7242	7254	7266	7278	7290	7302	7314	43°	2	4	6
47°	7314	7325	7337	7349	7361	7373	7385	7396	7408	7420	7431	42°	2	4	6
48°	7431	7443	7455	7466	7478	7490	7501	7513	7524	7536	7547	41°	2	4	6
49°	7547	7559	7570	7581	7593	7604	7615	7627	7638	7649	0.7660	40°	2	4	6
50°	0.7660	7672	7683	7694	7705	7716	7727	7738	7749	7760	7771	39°	2	4	6
51°	7771	7782	7793	7804	7815	7826	7837	7848	7859	7869	7880	38°	2	4	5
52°	7880	7891	7902	7912	7923	7934	7944	7955	7965	7976	7986	37°	2	4	5
53°	7986	7997	8007	8018	8028	8039	8049	8059	8070	8080	8090	36°	2	3	5
54°	8090	8100	8111	8121	8131	8141	8151	8161	8171	8181	0.8192	35°	2	3	5
55°	0.8192	8202	8211	8221	8231	8241	8251	8261	8271	8281	8290	34°	2	3	5
56°	8290	8300	8310	8320	8329	8339	8348	8358	8368	8377	8387	33°	2	3	5
57°	8387	8396	8406	8415	8425	8434	8443	8453	8462	8471	8480	32°	2	3	5
58°	8480	8490	8499	8508	8517	8526	8536	8545	8554	8563	8572	31°	2	3	5
59°	8572	8581	8590	8599	8607	8616	8625	8634	8643	8652	0.8660	30°	1	3	4
60°	0.8660	8669	8678	8686	8695	8704	8712	8721	8729	8738	8746	29°	1	3	4
61°	8746	8755	8763	8771	8780	8788	8796	8805	8813	8821	8829	28°	1	3	4
62°	8829	8838	8846	8854	8862	8870	8878	8886	8894	8902	8910	27°	1	3	4
63°	8910	8918	8926	8934	8942	8949	8957	8965	8973	8980	8988	26°	1	3	4
64°	8988	8996	9003	9011	9018	9026	9033	9041	9048	9056	0.9063	25°	1	3	4
65°	0.9063	9070	9078	9085	9092	9100	9107	9114	9121	9128	9135	24°	1	2	4
66°	9135	9143	9150	9157	9164	9171	9178	9184	9191	9198	9205	23°	1	2	3
67°	9205	9212	9219	9225	9232	9239	9245	9252	9259	9256	9272	22°	1	2	3
68°	9272	9278	9285	9291	9298	9304	9311	9317	9323	9330	9336	21°	1	2	3
69°	9336	9342	9348	9354	9361	9367	9373	9379	9383	9391	0.9397	20°	1	2	3
70 องศา	9397	9403	9409	9415	9421	9426	9432	9438	9444	9449	0.9455	19°	1	2	3
71°	9455	9461	9466	9472	9478	9483	9489	9494	9500	9505	9511	18°	1	2	3
72°	9511	9516	9521	9527	9532	9537	9542	9548	9553	9558	9563	17°	1	2	3
73°	9563	9568	9573	9578	9583	9588	9593	9598	9603	9608	9613	16°	1	2	2
74°	9613	9617	9622	9627	9632	9636	9641	9646	9650	9655	0.9659	15°	1	2	2
75°	9659	9664	9668	9673	9677	9681	9686	9690	9694	9699	9703	14°	1	1	2
76°	9703	9707	9711	9715	9720	9724	9728	9732	9736	9740	9744	13°	1	1	2
77°	9744	9748	9751	9755	9759	9763	9767	9770	9774	9778	9781	12°	1	1	2
78°	9781	9785	9789	9792	9796	9799	9803	9806	9810	9813	9816	11°	1	1	2
79°	9816	9820	9823	9826	9829	9833	9836	9839	9842	9845	0.9848	10°	1	1	2
80 °	0.9848	9851	9854	9857	9860	9863	9866	9869	9871	9874	9877	9°	0	1	1
81°	9877	9880	9882	9885	9888	9890	9893	9895	9898	9900	9903	8°	0	1	1
82°	9903	9905	9907	9910	9912	9914	9917	9919	9921	9923	9925	7°	0	1	1
83°	9925	9928	9930	9932	9934	9936	9938	9940	9942	9943	9945	6°	0	1	1
84°	9945	9947	9949	9951	9952	9954	9956	9957	9959	9960	9962	5 °	0	1	1
85°	9962	9963	9965	9966	9968	9969	9971	9972	9973	9974	9976	4°	0	0	1
86°	9976	9977	9978	9979	9980	9981	9982	9983	9984	9985	9986	3°	0	0	0
87°	9986	9987	9988	9989	9990	9990	9991	9992	9993	9993	9994	2°	0	0	0
88°	9994	9995	9995	9996	9996	9997	9997	9997	9998	9998	0.9998	1°	0	0	0
89°	9998	9999	9999	9999	9999	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	0°	0	0	0
90°	1.0000
บาป	60"	54"	48"	42"	36"	30"	24"	18"	12"	6"	0"	cos	1"	2"	3"

ในการหาค่าของไซน์และโคไซน์ของมุมที่ไม่ได้แสดงในตาราง จำเป็นต้องใช้การแก้ไข

ตอนนี้เราให้ตาราง Bradys สำหรับแทนเจนต์และโคแทนเจนต์ ประกอบด้วยค่าแทนเจนต์ของมุมตั้งแต่ 0 ถึง 76 องศาและโคแทนเจนต์ของมุมตั้งแต่ 14 ถึง 90 องศา

ตาราง Bradis สำหรับแทนเจนต์และโคแทนเจนต์

tg	0"	6"	12"	18"	24"	30"	36"	42"	48"	54"	60"	ctg	1"	2"	3"
											0	90°
0°	0,000	0017	0035	0052	0070	0087	0105	0122	0140	0157	0175	89°	3	6	9
1°	0175	0192	0209	0227	0244	0262	0279	0297	0314	0332	0349	88°	3	6	9
2°	0349	0367	0384	0402	0419	0437	0454	0472	0489	0507	0524	87°	3	6	9
3°	0524	0542	0559	0577	0594	0612	0629	0647	0664	0682	0699	86°	3	6	9
4°	0699	0717	0734	0752	0769	0787	0805	0822	0840	0857	0,0875	85°	3	6	9
5 °	0,0875	0892	0910	0928	0945	0963	0981	0998	1016	1033	1051	84°	3	6	9
6°	1051	1069	1086	1104	1122	1139	1157	1175	1192	1210	1228	83°	3	6	9
7°	1228	1246	1263	1281	1299	1317	1334	1352	1370	1388	1405	82°	3	6	9
8°	1405	1423	1441	1459	1477	1495	1512	1530	1548	1566	1584	81°	3	6	9
9°	1584	1602	1620	1638	1655	1673	1691	1709	1727	1745	0,1763	80 °	3	6	9
10°	0,1763	1781	1799	1817	1835	1853	1871	1890	1908	1926	1944	79°	3	6	9
11°	1944	1962	1980	1998	2016	2035	2053	2071	2089	2107	2126	78°	3	6	9
12°	2126	2144	2162	2180	2199	2217	2235	2254	2272	2290	2309	77°	3	6	9
13°	2309	2327	2345	2364	2382	2401	2419	2438	2456	2475	2493	76°	3	6	9
14°	2493	2512	2530	2549	2568	2586	2605	2623	2642	2661	0,2679	75°	3	6	9
15°	0,2679	2698	2717	2736	2754	2773	2792	2811	2830	2849	2867	74°	3	6	9
16°	2867	2886	2905	2924	2943	2962	2981	3000	3019	3038	3057	73°	3	6	9
17°	3057	3076	3096	3115	3134	3153	3172	3191	3211	3230	3249	72°	3	6	10
18°	3249	3269	3288	3307	3327	3346	3365	3385	3404	3424	3443	71°	3	6	10
19°	3443	3463	3482	3502	3522	3541	3561	3581	3600	3620	0,3640	70 องศา	3	7	10
20°	0,3640	3659	3679	3699	3719	3739	3759	3779	3799	3819	3839	69°	3	7	10
21°	3839	3859	3879	3899	3919	3939	3959	3979	4000	4020	4040	68°	3	7	10
22°	4040	4061	4081	4101	4122	4142	4163	4183	4204	4224	4245	67°	3	7	10
23°	4245	4265	4286	4307	4327	4348	4369	4390	4411	4431	4452	66°	3	7	10
24°	4452	4473	4494	4515	4536	4557	4578	4599	4621	4642	0,4663	65°	4	7	11
25°	0,4663	4684	4706	4727	4748	4770	4791	4813	4834	4856	4877	64°	4	7	11
26°	4877	4899	4921	4942	4964	4986	5008	5029	5051	5073	5095	63°	4	7	11
27°	5095	5117	5139	5161	5184	5206	5228	5250	5272	5295	5317	62°	4	7	11
28°	5317	5340	5362	5384	5407	5430	5452	5475	5498	5520	5543	61°	4	8	11
29°	5543	5566	5589	5612	5635	5658	5681	5704	5727	5750	0,5774	60°	4	8	12
30°	0,5774	5797	5820	5844	5867	5890	5914	5938	5961	5985	6009	59°	4	8	12
31°	6009	6032	6056	6080	6104	6128	6152	6176	6200	6224	6249	58°	4	8	12
32°	6249	6273	6297	6322	6346	6371	6395	6420	6445	6469	6494	57°	4	8	12
33°	6494	6519	6544	6569	6594	6619	6644	6669	6694	6720	6745	56°	4	8	13
34°	6745	6771	6796	6822	6847	6873	6899	6924	6950	6976	0,7002	55°	4	9	13
35°	0,7002	7028	7054	7080	7107	7133	7159	7186	7212	7239	7265	54°	4	8	13
36°	7265	7292	7319	7346	7373	7400	7427	7454	7481	7508	7536	53°	5	9	14°
37°	7536	7563	7590	7618	7646	7673	7701	7729	7757	7785	7813	52°	5	9	14
38°	7813	7841	7869	7898	7926	7954	7983	8012	8040	8069	8098	51°	5	9	14
39°	8098	8127	8156	8185	8214	8243	8273	8302	8332	8361	0,8391	50°	5	10	15
40°	0,8391	8421	8451	8481	8511	8541	8571	8601	8632	8662	0,8693	49°	5	10	15
41°	8693	8724	8754	8785	8816	8847	8878	8910	8941	8972	9004	48°	5	10	16
42°	9004	9036	9067	9099	9131	9163	9195	9228	9260	9293	9325	47°	6	11	16
43°	9325	9358	9391	9424	9457	9490	9523	9556	9590	9623	0,9657	46°	6	11	17
44°	9657	9691	9725	9759	9793	9827	9861	9896	9930	9965	1,0000	45 °	6	11	17
45 °	1,0000	0035	0070	0105	0141	0176	0212	0247	0283	0319	0355	44°	6	12	18
46°	0355	0392	0428	0464	0501	0538	0575	0612	0649	0686	0724	43°	6	12	18
47°	0724	0761	0799	0837	0875	0913	0951	0990	1028	1067	1106	42°	6	13	19
48°	1106	1145	1184	1224	1263	1303	1343	1383	1423	1463	1504	41°	7	13	20
49°	1504	1544	1585	1626	1667	1708	1750	1792	1833	1875	1,1918	40°	7	14	21
50°	1,1918	1960	2002	2045	2088	2131	2174	2218	2261	2305	2349	39°	7	14	22
51°	2349	2393	2437	2482	2527	2572	2617	2662	2708	2753	2799	38°	8	15	23
52°	2799	2846	2892	2938	2985	3032	3079	3127	3175	3222	3270	37°	8	16	24
53°	3270	3319	3367	3416	3465	3514	3564	3613	3663	3713	3764	36°	8	16	25
54°	3764	3814	3865	3916	3968	4019	4071	4124	4176	4229	1,4281	35°	9	17	26
55°	1,4281	4335	4388	4442	4496	4550	4605	4659	4715	4770	4826	34°	9	18	27
56°	4826	4882	4938	4994	5051	5108	5166	5224	5282	5340	5399	33°	10	19	29
57°	5399	5458	5517	5577	5637	5697	5757	5818	5880	5941	6003	32°	10	20	30
58°	6003	6066	6128	6191	6255	6319	6383	6447	6512	6577	6643	31°	11	21	32
59°	6643	6709	6775	6842	6909	6977	7045	7113	7182	7251	1,7321	30°	11	23	34
60°	1,732	1,739	1,746	1,753	1,760	1,767	1,775	1,782	1,789	1,797	1,804	29°	1	2	4
61°	1,804	1,811	1,819	1,827	1,834	1,842	1,849	1,857	1,865	1,873	1,881	28°	1	3	4
62°	1,881	1,889	1,897	1,905	1,913	1,921	1,929	1,937	1,946	1,954	1,963	27°	1	3	4
63°	1,963	1,971	1,980	1,988	1,997	2,006	2,014	2,023	2,032	2,041	2,05	26°	1	3	4
64°	2,050	2,059	2,069	2,078	2,087	2,097	2,106	2,116	2,125	2,135	2,145	25°	2	3	5
65°	2,145	2,154	2,164	2,174	2,184	2,194	2,204	2,215	2,225	2,236	2,246	24°	2	3	5
66°	2,246	2,257	2,267	2,278	2,289	2,3	2,311	2,322	2,333	2,344	2,356	23°	2	4	5
67°	2,356	2,367	2,379	2,391	2,402	2,414	2,426	2,438	2,450	2,463	2,475	22°	2	4	6
68°	2,475	2,488	2,5	2,513	2,526	2,539	2,552	2,565	2,578	2,592	2,605	21°	2	4	6
69°	2,605	2,619	2,633	2,646	2,66	2,675	2,689	2,703	2,718	2,733	2,747	20°	2	5	7
70 องศา	2,747	2,762	2,778	2,793	2,808	2,824	2,840	2,856	2,872	2,888	2,904	19°	3	5	8
71°	2,904	2,921	2,937	2,954	2,971	2,989	3,006	3,024	3,042	3,06	3,078	18°	3	6	9
72°	3,078	3,096	3,115	3,133	3,152	3,172	3,191	3,211	3,230	3,251	3,271	17°	3	6	10
73°	3,271	3,291	3,312	3,333	3,354	3,376							3	7	10
							3,398	3,42	3,442	3,465	3,487	16°	4	7	11
74°	3,487	3,511	3,534	3,558	3,582	3,606							4	8	12
							3,630	3,655	3,681	3,706	3,732	15°	4	8	13
75°	3,732	3,758	3,785	3,812	3,839	3,867							4	9	13
							3,895	3,923	3,952	3,981	4,011	14°	5	10	14
tg	60"	54"	48"	42"	36"	30"	24"	18"	12"	6"	0"	ctg	1"	2"	3"

วิธีใช้โต๊ะ Bradys

พิจารณาตาราง Bradys สำหรับไซน์และโคไซน์ ทุกอย่างที่เกี่ยวข้องกับไซนัสอยู่ที่ด้านบนและด้านซ้าย ถ้าเราต้องการโคไซน์ เราจะดูที่ด้านขวาล่างของตาราง

ในการหาค่าของไซน์ของมุม คุณต้องหาจุดตัดของแถวที่มีจำนวนองศาที่ต้องการในเซลล์ด้านซ้ายสุดและคอลัมน์ที่มีจำนวนนาทีในเซลล์ด้านบน

หากค่ามุมที่แน่นอนไม่อยู่ในตาราง Bradis เราจะใช้วิธีแก้ไข การแก้ไขสำหรับหนึ่ง สอง และสามนาทีจะแสดงในคอลัมน์ขวาสุดของตาราง ในการหาค่าไซน์ของมุมที่ไม่อยู่ในตาราง เราจะหาค่าที่ใกล้เคียงที่สุด หลังจากนั้นเราบวกหรือลบการแก้ไขที่สอดคล้องกับความแตกต่างระหว่างมุม

หากเรากำลังมองหาไซน์ของมุมที่มากกว่า 90 องศา ขั้นแรกเราจำเป็นต้องใช้สูตรการรีดิวซ์และจากนั้น - ตาราง Bradis

ตัวอย่าง. วิธีใช้ตาราง Bradis

ให้จำเป็นต้องหาค่าไซน์ของมุม 17 ° 44 " จากตาราง เราจะพบว่าค่าไซน์คือ 17 ° 42" และเพิ่มค่าแก้ไขเป็นเวลาสองนาที:

17° 44" - 17° 42" = 2" (ต้องการไอออนที่ถูกต้อง) บาป 17° 44" = 0 3040 + 0 . 0006 = 0 . 3046

หลักการทำงานกับโคไซน์ แทนเจนต์ และโคแทนเจนต์นั้นคล้ายคลึงกัน อย่างไรก็ตาม สิ่งสำคัญคือต้องจำเครื่องหมายของการแก้ไข

สำคัญ!

เมื่อคำนวณค่าของไซน์ การแก้ไขจะมีเครื่องหมายบวก และเมื่อคำนวณโคไซน์ การแก้ไขจะต้องใช้เครื่องหมายลบ

หากคุณสังเกตเห็นข้อผิดพลาดในข้อความ โปรดไฮไลต์แล้วกด Ctrl+Enter

ตารางฟังก์ชันตรีโกณมิติพื้นฐานสำหรับมุม 0, 30, 45, 60, 90, ... องศา

จากนิยามตรีโกณมิติของฟังก์ชัน $\sin$, $\cos$, $\tan$ และ $\cot$ เราสามารถหาค่าของมุม $0$ และ $90$ องศาได้:

$\sin⁡0°=0$, $\cos0°=1$, $\tan 0°=0$, $\cot 0°$ ไม่ได้กำหนดไว้;

$\sin90°=1$, $\cos90°=0$, $\cot90°=0$, $\tan 90°$ ไม่ได้กำหนดไว้

ในหลักสูตรเรขาคณิตของโรงเรียน เมื่อศึกษาสามเหลี่ยมมุมฉาก จะพบฟังก์ชันตรีโกณมิติของมุม $0°$, $30°$, $45°$, $60°$ และ $90°$

ค่าที่พบของฟังก์ชันตรีโกณมิติสำหรับมุมที่ระบุเป็นองศาและเรเดียนตามลำดับ ($0$, $\frac(\pi)(6)$, $\frac(\pi)(4)$, $\frac(\ pi)(3) $, $\frac(\pi)(2)$) เพื่อความสะดวกในการท่องจำและใช้งาน จะถูกป้อนลงในตารางที่ชื่อว่า ตารางตรีโกณมิติ, ตารางค่าพื้นฐานของฟังก์ชันตรีโกณมิติฯลฯ

เมื่อใช้สูตรการลดขนาด ตารางตรีโกณมิติสามารถขยายเป็นมุม 360°$ และ $2\pi$ เรเดียนตามลำดับ:

การใช้คุณสมบัติคาบของฟังก์ชันตรีโกณมิติ แต่ละมุมที่แตกต่างจากที่ทราบอยู่แล้วโดย $360°$ สามารถคำนวณและบันทึกลงในตารางได้ ตัวอย่างเช่น ฟังก์ชันตรีโกณมิติสำหรับมุม $0°$ จะมีค่าเท่ากันสำหรับมุม $0°+360°$ และสำหรับมุม $0°+2 \cdot 360°$ และสำหรับมุม $0°+3 \ cdot 360°$ และอื่นๆ

การใช้ตารางตรีโกณมิติ คุณสามารถกำหนดค่าของทุกมุมของวงกลมหนึ่งหน่วยได้

ในหลักสูตรเรขาคณิตของโรงเรียน ควรจะจดจำค่าพื้นฐานของฟังก์ชันตรีโกณมิติที่รวบรวมไว้ในตารางตรีโกณมิติเพื่อความสะดวกในการแก้ปัญหาเกี่ยวกับวิชาตรีโกณมิติ

การใช้โต๊ะ

ในตาราง ก็เพียงพอที่จะค้นหาฟังก์ชันตรีโกณมิติที่จำเป็นและค่าของมุมหรือเรเดียนที่ต้องการคำนวณฟังก์ชันนี้ ที่จุดตัดของแถวที่มีฟังก์ชันและคอลัมน์ที่มีค่า เราจะได้ค่าที่ต้องการของฟังก์ชันตรีโกณมิติของอาร์กิวเมนต์ที่กำหนด

ในรูป คุณสามารถดูวิธีการหาค่า $\cos⁡60°$ ซึ่งเท่ากับ $\frac(1)(2)$

ใช้ตารางตรีโกณมิติแบบขยายในทำนองเดียวกัน ข้อดีของการใช้งานคือ ดังที่ได้กล่าวไปแล้ว การคำนวณฟังก์ชันตรีโกณมิติของเกือบทุกมุม ตัวอย่างเช่น คุณสามารถหาค่า $\tan 1 380°=\tan (1 380°-360°)=\tan(1 020°-360°)=\tan(660°-360°)=\tan300 ได้อย่างง่ายดาย °$:

ตาราง Bradis ของฟังก์ชันตรีโกณมิติพื้นฐาน

ความสามารถในการคำนวณฟังก์ชันตรีโกณมิติของค่ามุมใดๆ ก็ตามสำหรับค่าจำนวนเต็มขององศาและค่าจำนวนเต็มเป็นนาทีทำให้สามารถใช้ตาราง Bradis ได้ ตัวอย่างเช่น ค้นหาค่า $\cos⁡34°7"$ ตารางแบ่งออกเป็น 2 ส่วนคือ ตารางค่า $\sin$ และ $\cos$ และตารางของ $\tan$ และ $\ ค่า cot$

ตาราง Bradis ทำให้สามารถรับค่าฟังก์ชันตรีโกณมิติโดยประมาณได้อย่างแม่นยำด้วยตำแหน่งทศนิยม 4 ตำแหน่ง

การใช้ตาราง Bradis

โดยใช้ตารางของ Bradys สำหรับไซน์ เราจะพบ $\sin⁡17°42"$ ในการทำเช่นนี้ ในคอลัมน์ทางด้านซ้ายของตารางไซน์และโคไซน์ เราจะหาค่าขององศา - $17°$ และใน บรรทัดบนสุด เราพบค่าของนาที - $42"$ ที่ทางแยกเราได้รับค่าที่ต้องการ:

$\sin17°42"=0.304$.

หากต้องการหาค่าของ $\sin17°44"$ คุณต้องใช้การแก้ไขที่ด้านขวาของตาราง ในกรณีนี้ คุณต้องเพิ่มค่าของ $42"$ ซึ่งอยู่ในตาราง การแก้ไขสำหรับ $2"$ ซึ่งเท่ากับ $0.0006$ เราได้รับ:

$\sin17°44"=0.304+0.0006=0.3046$.

ในการหาค่าของ $\sin17°47"$ เรายังใช้การแก้ไขทางด้านขวาของตาราง เฉพาะในกรณีนี้ เราจะนำค่าของ $\sin17°48"$ เป็นพื้นฐานแล้วลบค่าแก้ไขของ $1"$:

$\sin17°47"=0.3057-0.0003=0.3054$.

เมื่อคำนวณโคไซน์ เราทำการกระทำที่คล้ายกัน แต่เราดูที่องศาในคอลัมน์ขวาและนาทีในคอลัมน์ด้านล่างของตาราง ตัวอย่างเช่น $\cos20°=0.9397$

ไม่มีการแก้ไขค่าแทนเจนต์สูงถึง $90°$ และโคแทนเจนต์มุมเล็ก ตัวอย่างเช่น ลองหา $\tan 78°37"$ ซึ่งตามตารางคือ $4,967$

ในบทความเราจะเข้าใจอย่างถ่องแท้ว่าหน้าตาเป็นอย่างไร ตารางค่าตรีโกณมิติ ไซน์ โคไซน์ แทนเจนต์และโคแทนเจนต์. พิจารณาค่าพื้นฐานของฟังก์ชันตรีโกณมิติ จากมุม 0,30,45,60,90,...,360 องศา และมาดูวิธีการใช้ตารางเหล่านี้ในการคำนวณค่าของฟังก์ชันตรีโกณมิติกัน
พิจารณาก่อน ตารางโคไซน์ ไซน์ แทนเจนต์ และโคแทนเจนต์จากมุม 0, 30, 45, 60, 90,.. องศา คำจำกัดความของปริมาณเหล่านี้ทำให้สามารถกำหนดค่าฟังก์ชันของมุม 0 และ 90 องศาได้:

บาป 0 0 \u003d 0, cos 0 0 \u003d 1. tg 0 0 \u003d 0, โคแทนเจนต์ของ 0 0 จะไม่แน่นอน
sin 90 0 = 1, cos 90 0 =0, ctg90 0 = 0, แทนเจนต์ของ 90 0 จะไม่ถูกกำหนด

ถ้าเราเอาสามเหลี่ยมมุมฉากที่มีมุมตั้งแต่ 30 ถึง 90 องศา เราได้รับ:

บาป 30 0 = 1/2, cos 30 0 = √3/2, tg 30 0 = √3/3, ctg 30 0 = √3
บาป 45 0 = √2/2, cos 45 0 = √2/2, tg 45 0 = 1, ctg 45 0 = 1
บาป 60 0 = √3/2, cos 60 0 = 1/2, tg 60 0 =√3, ctg 60 0 = √3/3

เราแสดงค่าที่ได้รับทั้งหมดในรูปแบบ ตารางตรีโกณมิติ:

ตารางของไซน์ โคไซน์ แทนเจนต์ และโคแทนเจนต์!

หากเราใช้สูตรลดตารางของเราจะเพิ่มขึ้นค่าสำหรับมุมสูงถึง 360 องศาจะถูกเพิ่ม จะมีลักษณะดังนี้:

ตารางจะเพิ่มขึ้นตามคุณสมบัติของคาบหากเราแทนที่มุมด้วย 0 0 +360 0 *z .... 330 0 +360 0 *z โดยที่ z เป็นจำนวนเต็ม ในตารางนี้ เป็นไปได้ที่จะคำนวณค่าของมุมทั้งหมดที่สอดคล้องกับจุดในวงกลมเดียว

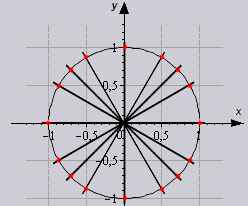
มาดูวิธีการใช้ตารางในการแก้ปัญหากันอย่างชัดเจน
ทุกอย่างง่ายมาก เนื่องจากค่าที่เราต้องการจะอยู่ที่จุดตัดกันของเซลล์ที่เราต้องการ ตัวอย่างเช่น ลอง cos ของมุม 60 องศา ในตารางจะมีลักษณะดังนี้:

ในตารางสุดท้ายของค่าหลักของฟังก์ชันตรีโกณมิติ เราดำเนินการในลักษณะเดียวกัน แต่ในตารางนี้ เป็นไปได้ที่จะหาว่าค่าแทนเจนต์จากมุม 1,020 องศาจะเป็นเท่าไหร่ = -√3 ลองดู 1020 0 = 300 0 +360 0 *2 มาหาโต๊ะกันเถอะ

ใช้การค้นหาค่ามุมตรีโกณมิติที่แม่นยำเป็นนาทีมากขึ้น คำแนะนำโดยละเอียดเกี่ยวกับวิธีการใช้งานในหน้า

โต๊ะแบรดดิส สำหรับไซน์ โคไซน์ แทนเจนต์ และโคแทนเจนต์

ตารางของ Bradys แบ่งออกเป็นหลายส่วน ประกอบด้วยตารางของโคไซน์และไซน์ แทนเจนต์และโคแทนเจนต์ ซึ่งแบ่งออกเป็นสองส่วน (tg ของมุมสูงสุด 90 องศาและ ctg ของมุมเล็ก)

ไซน์และโคไซน์

มุม tg เริ่มต้นจาก 0 0 สิ้นสุด 76 0 มุม ctg เริ่มต้นจาก 14 0 สิ้นสุด 90 0

tg สูงถึง 90 0 และ ctg มุมเล็ก ๆ

มาดูวิธีการใช้ตาราง Bradis ในการแก้ปัญหากัน

หาค่ากำหนดบาปกัน (กำหนดในคอลัมน์จากขอบด้านซ้าย) 42 นาที (กำหนดอยู่บรรทัดบนสุด) โดยการข้ามเรากำลังหาการกำหนด มันคือ = 0.3040

ค่าของนาทีจะถูกระบุด้วยช่วงเวลาหกนาที เกิดอะไรขึ้นถ้าค่าที่เราต้องการอยู่ภายในช่วงเวลานี้ ลองใช้เวลา 44 นาทีและมีเพียง 42 ในตารางเท่านั้น เราใช้ 42 เป็นพื้นฐานและใช้คอลัมน์เพิ่มเติมทางด้านขวาแก้ไขครั้งที่ 2 และเพิ่มเป็น 0.3040 + 0.0006 เราได้ 0.3046

ด้วยบาป 47 นาที เราใช้เวลา 48 นาทีเป็นพื้นฐาน และลบ 1 การแก้ไขออกจากค่านั้น นั่นคือ 0.3057 - 0.0003 = 0.3054

เมื่อคำนวณ cos เราทำงานคล้ายกับบาป เพียงแต่เราเอาแถวล่างของตารางเป็นฐาน ตัวอย่างเช่น cos 20 0 = 0.9397

ค่า tg ของมุมสูงถึง 90 0 และมุมเล็ก ๆ นั้นถูกต้องและไม่มีการแก้ไขในนั้น ตัวอย่างเช่น ค้นหา tg 78 0 37min = 4.967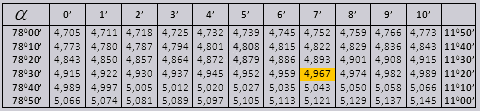


และ ctg 20 0 13 นาที = 25.83

ที่นี่เราได้พิจารณาตารางตรีโกณมิติหลักแล้ว เราหวังว่าข้อมูลนี้จะเป็นประโยชน์อย่างยิ่งสำหรับคุณ คำถามของคุณบนโต๊ะ หากมี อย่าลืมเขียนในความคิดเห็น!

หมายเหตุ: กันชนผนัง - แผ่นกันชนสำหรับปกป้องผนัง (http://www.spi-polymer.ru/otboyniki/)

พูดง่ายๆ ก็คือ ผักที่ปรุงในน้ำตามสูตรพิเศษ ฉันจะพิจารณาสององค์ประกอบเริ่มต้น (สลัดผักและน้ำ) และผลลัพธ์ที่ได้คือ Borscht ในเชิงเรขาคณิต นี่สามารถแสดงเป็นรูปสี่เหลี่ยมผืนผ้าโดยที่ด้านหนึ่งหมายถึงผักกาดหอม อีกด้านหนึ่งหมายถึงน้ำ ผลรวมของทั้งสองข้างนี้จะแสดงถึง Borscht เส้นทแยงมุมและพื้นที่ของสี่เหลี่ยมผืนผ้า "บอร์ชท์" เป็นแนวคิดทางคณิตศาสตร์ล้วนๆ และไม่เคยใช้ในสูตรบอร์ชท์

ผักกาดหอมและน้ำกลายเป็น Borscht ในแง่ของคณิตศาสตร์ได้อย่างไร ผลรวมของสองส่วนจะกลายเป็นตรีโกณมิติได้อย่างไร? เพื่อให้เข้าใจสิ่งนี้ เราจำเป็นต้องมีฟังก์ชันมุมเชิงเส้น

คุณจะไม่พบอะไรเกี่ยวกับฟังก์ชันมุมเชิงเส้นในหนังสือเรียนคณิตศาสตร์ แต่หากไม่มีพวกเขา ก็ไม่มีคณิตศาสตร์ กฎของคณิตศาสตร์ เช่นเดียวกับกฎธรรมชาติ ทำงานไม่ว่าเราจะรู้ว่ามีอยู่จริงหรือไม่ก็ตาม

ฟังก์ชันเชิงมุมเชิงเส้นคือกฎของการบวกดูว่าพีชคณิตเปลี่ยนเป็นเรขาคณิตได้อย่างไร และเรขาคณิตเปลี่ยนเป็นตรีโกณมิติได้อย่างไร

เป็นไปได้ไหมที่จะทำโดยไม่มีฟังก์ชันเชิงมุมเชิงเส้น? คุณสามารถทำได้เพราะนักคณิตศาสตร์ยังคงจัดการได้โดยไม่มีพวกเขา เคล็ดลับของนักคณิตศาสตร์อยู่ที่การที่พวกเขามักจะบอกเราเกี่ยวกับปัญหาที่พวกเขาแก้ได้ด้วยตัวเองเท่านั้น และไม่เคยบอกเราเกี่ยวกับปัญหาที่พวกเขาแก้ไม่ได้ ดู. หากเราทราบผลลัพธ์ของการบวกและเทอมหนึ่ง เราจะใช้การลบเพื่อหาอีกเทอมหนึ่ง ทุกอย่าง. เราไม่ทราบปัญหาอื่น ๆ และเราไม่สามารถแก้ไขได้ จะทำอย่างไรถ้าเรารู้เพียงผลลัพธ์ของการบวกและไม่รู้ทั้งสองคำ? ในกรณีนี้ ผลลัพธ์ของการบวกจะต้องแยกออกเป็นสองพจน์โดยใช้ฟังก์ชันเชิงมุมเชิงเส้น นอกจากนี้ เราเองก็เลือกพจน์หนึ่งที่สามารถเป็นได้ และฟังก์ชันเชิงมุมเชิงเส้นแสดงว่าเทอมที่สองควรเป็นเท่าใด เพื่อให้ผลลัพธ์ของการบวกกลายเป็นสิ่งที่เราต้องการอย่างแท้จริง สามารถมีจำนวนคู่ของเงื่อนไขดังกล่าวได้เป็นอนันต์ ในชีวิตประจำวัน เราทำได้ดีมากโดยไม่แบ่งแยกผลรวม การลบก็เพียงพอแล้วสำหรับเรา แต่ในการศึกษาทางวิทยาศาสตร์เกี่ยวกับกฎแห่งธรรมชาติ การขยายผลรวมเป็นเงื่อนไขนั้นมีประโยชน์มาก

กฎการบวกอีกข้อที่นักคณิตศาสตร์ไม่ชอบพูดถึง (เคล็ดลับอีกอย่างของพวกเขา) กำหนดให้เงื่อนไขต้องมีหน่วยวัดเหมือนกัน สำหรับผักกาดหอม น้ำ และบอร์ช อาจเป็นหน่วยน้ำหนัก ปริมาตร ต้นทุน หรือหน่วยวัด

รูปแสดงความแตกต่างสองระดับสำหรับคณิตศาสตร์ ระดับแรกคือความแตกต่างในด้านตัวเลขซึ่งระบุไว้ เอ, ข, ค. นี่คือสิ่งที่นักคณิตศาสตร์ทำ ระดับที่สองคือความแตกต่างในพื้นที่ของหน่วยวัดซึ่งแสดงในวงเล็บเหลี่ยมและระบุด้วยตัวอักษร ยู. นี่คือสิ่งที่นักฟิสิกส์ทำ เราสามารถเข้าใจระดับที่สาม - ความแตกต่างในขอบเขตของวัตถุที่อธิบายไว้ วัตถุที่แตกต่างกันสามารถมีจำนวนหน่วยวัดเท่ากันได้ เรื่องนี้สำคัญแค่ไหน เราสามารถเห็นได้จากตัวอย่างตรีโกณมิติ Borscht หากเราเพิ่มตัวห้อยลงในสัญกรณ์เดียวกันสำหรับหน่วยการวัดของวัตถุต่างๆ เราสามารถพูดได้อย่างชัดเจนว่าปริมาณทางคณิตศาสตร์ใดที่อธิบายวัตถุนั้น ๆ และการเปลี่ยนแปลงเมื่อเวลาผ่านไปหรือเกี่ยวข้องกับการกระทำของเราอย่างไร จดหมาย Wฉันจะทำเครื่องหมายน้ำด้วยตัวอักษร สฉันจะทำเครื่องหมายสลัดด้วยตัวอักษร บี- บอร์ช นี่คือหน้าตาของฟังก์ชันมุมเชิงเส้นของบอร์ชท์

ถ้าเรานำน้ำบางส่วนและบางส่วนของสลัดมารวมกันจะกลายเป็น Borscht หนึ่งเสิร์ฟ ที่นี่ฉันแนะนำให้คุณหยุดพักจาก Borscht และระลึกถึงวัยเด็กอันห่างไกลของคุณ จำได้ไหมว่าเราถูกสอนให้รวมกระต่ายกับเป็ดเข้าด้วยกันได้อย่างไร? จำเป็นต้องค้นหาว่าจะมีสัตว์กี่ตัว แล้วเราถูกสอนให้ทำอะไร? เราถูกสอนให้แยกหน่วยจากตัวเลขและบวกตัวเลข ใช่ คุณสามารถเพิ่มหมายเลขใด ๆ ลงในหมายเลขอื่นได้ นี่เป็นเส้นทางตรงสู่ความหมกหมุ่นของคณิตศาสตร์สมัยใหม่ - เราไม่เข้าใจว่าอะไร ไม่ชัดเจนว่าทำไม และเราเข้าใจได้ไม่ดีนักว่าสิ่งนี้เกี่ยวข้องกับความเป็นจริงอย่างไร เนื่องจากความแตกต่างสามระดับ นักคณิตศาสตร์จึงดำเนินการเพียงระดับเดียวเท่านั้น จะถูกต้องมากขึ้นในการเรียนรู้วิธีการย้ายจากหน่วยการวัดหนึ่งไปยังอีกหน่วยหนึ่ง

และกระต่าย เป็ด และสัตว์เล็กๆ ก็สามารถแบ่งได้เป็นชิ้นๆ หน่วยวัดทั่วไปหนึ่งหน่วยสำหรับวัตถุต่างๆ ช่วยให้เรารวมเข้าด้วยกันได้ นี่เป็นปัญหารุ่นเด็ก ลองดูปัญหาที่คล้ายกันสำหรับผู้ใหญ่ คุณจะได้อะไรเมื่อคุณเพิ่มกระต่ายและเงิน? มีวิธีแก้ไขที่เป็นไปได้สองวิธีที่นี่

ตัวเลือกแรก. เรากำหนดมูลค่าตลาดของกระต่ายและเพิ่มเป็นเงินสดที่มีอยู่ เราได้รับมูลค่ารวมของความมั่งคั่งของเราในแง่ของเงิน

ตัวเลือกที่สอง. คุณสามารถเพิ่มจำนวนกระต่ายในจำนวนธนบัตรที่เรามีได้ เราจะได้จำนวนสังหาริมทรัพย์เป็นชิ้นๆ

อย่างที่คุณเห็น กฎการบวกเดียวกันอนุญาตให้คุณได้ผลลัพธ์ที่แตกต่างกัน ทุกอย่างขึ้นอยู่กับสิ่งที่เราต้องการทราบ

แต่กลับไปที่ Borscht ของเรา ตอนนี้เราสามารถเห็นสิ่งที่จะเกิดขึ้นสำหรับค่าต่างๆ ของมุมของฟังก์ชันมุมเชิงเส้น

มุมเป็นศูนย์ มีสลัดแต่ไม่มีน้ำ เราไม่สามารถปรุง Borscht ได้ ปริมาณ Borscht ยังเป็นศูนย์ นี่ไม่ได้หมายความว่าศูนย์ Borscht เท่ากับศูนย์น้ำ Zero borsch สามารถเป็นศูนย์สลัดได้ (มุมขวา)

สำหรับฉันเป็นการส่วนตัว นี่คือข้อพิสูจน์หลักทางคณิตศาสตร์ว่า ศูนย์จะไม่เปลี่ยนหมายเลขเมื่อเพิ่ม นี่เป็นเพราะการเพิ่มตัวเองเป็นไปไม่ได้ถ้ามีเพียงหนึ่งเทอมและไม่มีเทอมที่สอง คุณสามารถเชื่อมโยงสิ่งนี้ได้ตามที่คุณต้องการ แต่จำไว้ - การดำเนินการทางคณิตศาสตร์ทั้งหมดที่มีศูนย์นั้นถูกคิดค้นโดยนักคณิตศาสตร์เอง ดังนั้นให้ทิ้งตรรกะของคุณและยัดเยียดคำจำกัดความที่นักคณิตศาสตร์คิดค้นขึ้นอย่างโง่เขลา: "การหารด้วยศูนย์เป็นไปไม่ได้", "จำนวนใด ๆ ที่คูณด้วยศูนย์ เท่ากับศูนย์" , "หลังจุดศูนย์" และเรื่องไร้สาระอื่นๆ พอจะจำได้เมื่อศูนย์ไม่ใช่ตัวเลขและคุณจะไม่มีคำถามว่าศูนย์เป็นจำนวนธรรมชาติหรือไม่เพราะคำถามดังกล่าวโดยทั่วไปจะสูญเสียความหมายทั้งหมด: เราจะพิจารณาตัวเลขที่ไม่ใช่ตัวเลขได้อย่างไร . มันเหมือนกับการถามว่าสีอะไรเป็นแอตทริบิวต์สีที่มองไม่เห็น การเพิ่มศูนย์ให้กับตัวเลขก็เหมือนกับการระบายสีที่ไม่มีอยู่จริง พวกเขาโบกแปรงแห้งและบอกทุกคนว่า "เราทาสีแล้ว" แต่ฉันพูดเพ้อเจ้อเล็กน้อย

มุมมีค่ามากกว่าศูนย์แต่น้อยกว่าสี่สิบห้าองศา ผักสลัดมีเยอะแต่น้ำน้อย เป็นผลให้เราได้รับ Borscht หนา

มุมคือสี่สิบห้าองศา เรามีน้ำและผักกาดหอมในปริมาณที่เท่ากัน นี่คือ Borscht ที่สมบูรณ์แบบ (ขอให้พ่อครัวยกโทษให้ฉันมันเป็นแค่คณิตศาสตร์)

มุมมีค่ามากกว่าสี่สิบห้าองศาแต่น้อยกว่าเก้าสิบองศา เรามีน้ำเยอะและผักกาดน้อย รับของเหลว Borscht

มุมฉาก. เรามีน้ำ เหลือแต่ความทรงจำของผักกาดหอม เมื่อเราวัดมุมจากเส้นที่เคยทำเครื่องหมายผักกาดหอมต่อไป เราไม่สามารถปรุง Borscht ได้ ปริมาณ Borscht เป็นศูนย์ ในกรณีนี้ให้ถือและดื่มน้ำในขณะที่มี)))

ที่นี่. บางอย่างเช่นนี้ ฉันสามารถเล่าเรื่องอื่น ๆ ที่นี่ที่จะเกินความเหมาะสมได้ที่นี่

เพื่อนทั้งสองมีส่วนแบ่งในธุรกิจร่วมกัน หลังจากการสังหารหนึ่งในนั้น ทุกสิ่งทุกอย่างก็ไปสู่อีกคนหนึ่ง

การเกิดขึ้นของคณิตศาสตร์บนโลกของเรา

เรื่องราวทั้งหมดนี้เล่าในภาษาของคณิตศาสตร์โดยใช้ฟังก์ชันเชิงมุมเชิงเส้น คราวหน้าผมจะแสดงให้คุณเห็นตำแหน่งที่แท้จริงของฟังก์ชันเหล่านี้ในโครงสร้างของคณิตศาสตร์ ในระหว่างนี้ ให้กลับไปที่ตรีโกณมิติของ Borscht และพิจารณาการคาดคะเน

วันเสาร์ที่ 26 ตุลาคม 2019

วันพุธที่ 7 สิงหาคม 2019

เมื่อจบการสนทนาเกี่ยวกับ เราต้องพิจารณาเซตอนันต์ ให้แนวคิดว่า "อินฟินิตี้" มีผลกับนักคณิตศาสตร์ เหมือนงูเหลือมบนกระต่าย ความน่ากลัวที่สั่นไหวของอินฟินิตี้ทำให้นักคณิตศาสตร์ขาดสามัญสำนึก นี่คือตัวอย่าง:

แหล่งที่มาเดิมตั้งอยู่ อัลฟ่าหมายถึงจำนวนจริง เครื่องหมายเท่ากับในนิพจน์ข้างต้นระบุว่าหากคุณเพิ่มตัวเลขหรืออนันต์ให้กับอนันต์ ไม่มีอะไรจะเปลี่ยนแปลง ผลลัพธ์จะเป็นอนันต์เดียวกัน หากเราใช้เซตจำนวนนับไม่ถ้วนเป็นตัวอย่าง ตัวอย่างที่พิจารณาสามารถแสดงได้ดังนี้:

เพื่อพิสูจน์กรณีของพวกเขาด้วยสายตา นักคณิตศาสตร์ได้คิดค้นวิธีการต่างๆ มากมาย โดยส่วนตัวแล้ว ฉันมองว่าวิธีการทั้งหมดนี้เป็นการเต้นรำของหมอผีกับรำมะนา โดยพื้นฐานแล้ว พวกเขาทั้งหมดมาจากความจริงที่ว่าห้องพักบางห้องไม่ได้ถูกครอบครองและมีแขกใหม่เข้ามาตั้งรกราก หรือแขกบางคนถูกโยนออกไปที่ทางเดินเพื่อให้มีที่ว่างสำหรับแขก (อย่างมนุษย์ปุถุชน) ฉันนำเสนอมุมมองของฉันเกี่ยวกับการตัดสินใจดังกล่าวในรูปแบบของเรื่องราวที่ยอดเยี่ยมเกี่ยวกับสาวผมบลอนด์ เหตุผลของฉันขึ้นอยู่กับอะไร? การย้ายผู้เข้าชมจำนวนไม่ จำกัด ต้องใช้เวลาเป็นอนันต์ หลังจากที่เราออกจากห้องพักแขกห้องแรกแล้ว ผู้มาเยี่ยมคนหนึ่งจะเดินไปตามทางเดินจากห้องของเขาไปยังห้องถัดไปจนกว่าจะหมดเวลา แน่นอนว่าปัจจัยด้านเวลาอาจถูกมองข้ามไปอย่างโง่เขลา แต่สิ่งนี้จะมาจากหมวดหมู่ของ "กฎหมายไม่ได้เขียนขึ้นสำหรับคนโง่" ทุกอย่างขึ้นอยู่กับสิ่งที่เรากำลังทำ: การปรับความเป็นจริงให้เป็นทฤษฎีทางคณิตศาสตร์หรือในทางกลับกัน

"โรงแรมไม่มีที่สิ้นสุด" คืออะไร? อินน์แบบอินฟินิตี้คือโรงแรมขนาดเล็กที่มีจำนวนตำแหน่งว่างเสมอ ไม่ว่าจะมีห้องว่างกี่ห้องก็ตาม หากห้องทั้งหมดในโถงทางเดินที่ไม่มีที่สิ้นสุด "สำหรับผู้มาเยี่ยม" ถูกครอบครอง มีโถงทางเดินที่ไม่มีที่สิ้นสุดอีกแห่งที่มีห้องสำหรับ "แขก" จะมีทางเดินดังกล่าวจำนวนไม่สิ้นสุด ในเวลาเดียวกัน "โรงแรมที่ไม่มีที่สิ้นสุด" มีจำนวนชั้นที่ไม่มีที่สิ้นสุดในอาคารจำนวนไม่สิ้นสุดบนดาวเคราะห์จำนวนอนันต์ในจักรวาลจำนวนอนันต์ที่สร้างขึ้นโดยพระเจ้าจำนวนอนันต์ ในทางกลับกัน นักคณิตศาสตร์ไม่สามารถย้ายออกจากปัญหาซ้ำซากจำเจในแต่ละวัน: พระเจ้าอัลลอฮ์ - พระพุทธเจ้าเป็นเพียงแห่งเดียวเสมอ โรงแรมเป็นหนึ่ง ทางเดินเป็นเพียงแห่งเดียว ดังนั้นนักคณิตศาสตร์จึงพยายามเล่นปาหี่เลขลำดับของห้องพักในโรงแรม ทำให้เราเชื่อว่าเป็นไปได้ที่จะ "ผลักห้องที่ยังไม่ได้ผลัก"

ฉันจะสาธิตตรรกะของการให้เหตุผลกับคุณโดยใช้ตัวอย่างชุดจำนวนธรรมชาติอนันต์ ก่อนอื่น คุณต้องตอบคำถามง่ายๆ ก่อน: มีชุดจำนวนธรรมชาติกี่ชุด - หนึ่งชุดหรือหลายชุด ไม่มีคำตอบที่ถูกต้องสำหรับคำถามนี้ เนื่องจากเราเป็นผู้คิดค้นตัวเลขขึ้นมาเอง จึงไม่มีตัวเลขในธรรมชาติ ใช่ ธรรมชาติรู้วิธีนับอย่างสมบูรณ์แบบ แต่สำหรับสิ่งนี้ เธอใช้เครื่องมือทางคณิตศาสตร์อื่นๆ ที่เราไม่คุ้นเคย ตามที่ธรรมชาติคิด ฉันจะบอกคุณอีกครั้ง เนื่องจากเราประดิษฐ์ตัวเลข เราเองจะเป็นผู้กำหนดจำนวนธรรมชาติที่มีอยู่จำนวนกี่ชุด พิจารณาทั้งสองทางเลือก เนื่องจากเหมาะสมกับนักวิทยาศาสตร์ตัวจริง

ตัวเลือกที่หนึ่ง "ให้เราได้รับ" ชุดตัวเลขธรรมชาติชุดเดียวที่วางอยู่บนหิ้งอย่างสงบ เรานำชุดนี้จากชั้นวาง แค่นั้นแหละ ไม่มีตัวเลขธรรมชาติอื่น ๆ เหลืออยู่บนหิ้งและไม่มีที่ไหนเลยที่จะนำไปใช้ เราไม่สามารถเพิ่มหนึ่งชุดในชุดนี้ เนื่องจากเรามีอยู่แล้ว ถ้าคุณต้องการจริงๆ? ไม่มีปัญหา. เราสามารถนำหน่วยจากชุดที่เราถ่ายไปแล้วกลับไปที่หิ้งได้ หลังจากนั้นเราสามารถนำหน่วยจากชั้นวางและเพิ่มไปยังสิ่งที่เราเหลือได้ เป็นผลให้เราได้รับชุดจำนวนธรรมชาติที่ไม่สิ้นสุดอีกครั้ง คุณสามารถเขียนการปรับเปลี่ยนทั้งหมดของเราดังนี้:

ฉันได้เขียนการดำเนินการในรูปแบบพีชคณิตและสัญกรณ์ทฤษฎีเซต โดยแสดงรายการองค์ประกอบของเซตอย่างละเอียด ตัวห้อยระบุว่าเรามีชุดตัวเลขธรรมชาติชุดเดียวเท่านั้น ปรากฎว่าชุดของจำนวนธรรมชาติจะไม่เปลี่ยนแปลงก็ต่อเมื่อถูกลบออกจากมันและเพิ่มจำนวนเดียวกัน

ตัวเลือกที่สอง เรามีชุดตัวเลขธรรมชาติมากมายหลายชุดบนหิ้ง ฉันขอเน้นย้ำว่า - แตกต่างแม้ว่าจะแยกไม่ออกก็ตาม เราใช้หนึ่งในชุดเหล่านี้ จากนั้นเราก็นำตัวเลขธรรมชาติชุดหนึ่งมาบวกกับชุดที่เราถ่ายไปแล้ว เรายังบวกจำนวนธรรมชาติสองชุดได้อีกด้วย นี่คือสิ่งที่เราได้รับ:

ตัวห้อย "หนึ่ง" และ "สอง" ระบุว่าองค์ประกอบเหล่านี้เป็นของชุดที่ต่างกัน ใช่ หากคุณเพิ่มชุดหนึ่งไปยังชุดที่ไม่มีที่สิ้นสุด ผลลัพธ์จะเป็นชุดที่ไม่มีที่สิ้นสุดด้วย แต่จะไม่เหมือนกับชุดเดิม หากมีการเพิ่มชุดอนันต์อื่นในชุดอนันต์ชุดหนึ่ง ผลลัพธ์จะเป็นชุดอนันต์ชุดใหม่ที่ประกอบด้วยองค์ประกอบของสองชุดแรก

ชุดของตัวเลขธรรมชาติใช้สำหรับการนับในลักษณะเดียวกับไม้บรรทัดสำหรับการวัด ทีนี้ลองนึกภาพว่าคุณได้บวกหนึ่งเซนติเมตรเข้ากับไม้บรรทัดแล้ว นี่จะเป็นบรรทัดอื่นแล้วไม่เท่ากับเส้นเดิม

คุณสามารถยอมรับหรือไม่ยอมรับเหตุผลของฉัน - นี่คือธุรกิจของคุณเอง แต่ถ้าคุณเคยเจอปัญหาทางคณิตศาสตร์ ลองคิดดูว่าคุณกำลังอยู่บนเส้นทางของการใช้เหตุผลผิดๆ หรือไม่ ซึ่งถูกเหยียบย่ำโดยนักคณิตศาสตร์รุ่นต่อรุ่น ท้ายที่สุด ชั้นเรียนคณิตศาสตร์ อย่างแรกเลย สร้างแบบแผนที่มั่นคงของการคิดในตัวเรา จากนั้นจึงเพิ่มความสามารถทางจิตให้กับเรา (หรือในทางกลับกัน พวกเขากีดกันการคิดอย่างอิสระ)

pozg.ru

วันอาทิตย์ที่ 4 สิงหาคม 2019

ฉันกำลังเขียนบทความเกี่ยวกับบทความเกี่ยวกับและเห็นข้อความที่ยอดเยี่ยมนี้ใน Wikipedia:

เราอ่านว่า: "... พื้นฐานทางทฤษฎีที่ร่ำรวยของคณิตศาสตร์แบบบาบิโลนไม่มีคุณลักษณะแบบองค์รวมและถูกลดทอนเป็นชุดของเทคนิคที่แตกต่างกัน ปราศจากระบบทั่วไปและฐานหลักฐาน"

ว้าว! เราฉลาดแค่ไหน และมองเห็นข้อบกพร่องของผู้อื่นได้ดีเพียงใด การที่เรามองคณิตศาสตร์สมัยใหม่ในบริบทเดียวกันนั้นยังอ่อนแออยู่หรือไม่? การถอดความข้อความข้างต้นเล็กน้อย โดยส่วนตัว ฉันได้รับสิ่งต่อไปนี้:

พื้นฐานทางทฤษฎีที่เข้มข้นของคณิตศาสตร์สมัยใหม่ไม่ได้มีลักษณะแบบองค์รวมและถูกลดขนาดให้เป็นชุดของส่วนต่างๆ ที่แตกต่างกัน ปราศจากระบบทั่วไปและฐานหลักฐาน

ฉันจะไม่ไปไกลเพื่อยืนยันคำพูดของฉัน - มีภาษาและอนุสัญญาที่แตกต่างจากภาษาและอนุสัญญาของสาขาคณิตศาสตร์อื่น ๆ อีกมากมาย ชื่อเดียวกันในสาขาคณิตศาสตร์ที่แตกต่างกันสามารถมีความหมายต่างกัน ฉันต้องการอุทิศวงจรการตีพิมพ์ทั้งหมดให้กับความผิดพลาดที่ชัดเจนที่สุดของคณิตศาสตร์สมัยใหม่ เจอกันเร็วๆนี้.

วันเสาร์ที่ 3 สิงหาคม 2019

จะแบ่งเซตออกเป็นเซตย่อยได้อย่างไร? ในการดำเนินการนี้ คุณต้องป้อนหน่วยวัดใหม่ ซึ่งมีอยู่ในองค์ประกอบบางอย่างของชุดที่เลือก ขอ​พิจารณา​ตัว​อย่าง.

ขอให้มีกันเยอะๆนะครับ แต่ประกอบด้วยสี่คน ชุดนี้สร้างขึ้นบนพื้นฐานของ "คน" มากำหนดองค์ประกอบของชุดนี้ผ่านตัวอักษร เอตัวห้อยที่มีตัวเลขจะแสดงเลขลำดับของแต่ละคนในชุดนี้ มาแนะนำหน่วยวัดใหม่ "ลักษณะทางเพศ" และแสดงด้วยตัวอักษร ข. เนื่องจากลักษณะทางเพศมีอยู่ในทุกคน เราจึงคูณแต่ละองค์ประกอบของชุด แต่เกี่ยวกับเพศ ข. สังเกตว่าชุด "คน" ของเราตอนนี้กลายเป็นชุด "คนที่มีเพศ" แล้ว หลังจากนั้นเราสามารถแบ่งลักษณะทางเพศเป็นเพศชายได้ bmและของผู้หญิง bwลักษณะทางเพศ ตอนนี้ เราสามารถใช้ตัวกรองทางคณิตศาสตร์ได้: เราเลือกลักษณะทางเพศอย่างใดอย่างหนึ่งเหล่านี้ ไม่สำคัญว่าตัวผู้หรือตัวเมียตัวใด หากมีอยู่ในบุคคล เราก็คูณมันด้วยหนึ่ง ถ้าไม่มีเครื่องหมายดังกล่าว เราจะคูณมันด้วยศูนย์ แล้วเราก็ใช้คณิตศาสตร์ของโรงเรียนตามปกติ ดูสิ่งที่เกิดขึ้น

หลังจากการคูณ การลดลง และการจัดเรียงใหม่ เราได้ชุดย่อยสองชุด: ชุดย่อยเพศผู้ bmและส่วนย่อยของผู้หญิง bw. ในทำนองเดียวกันนักคณิตศาสตร์ให้เหตุผลเมื่อพวกเขาใช้ทฤษฎีเซตในทางปฏิบัติ แต่พวกเขาไม่ให้เราลงรายละเอียด แต่ให้ผลลัพธ์ที่สมบูรณ์แก่เรา - "ผู้คนจำนวนมากประกอบด้วยกลุ่มย่อยของผู้ชายและกลุ่มย่อยของผู้หญิง" โดยปกติคุณอาจมีคำถามว่าคณิตศาสตร์ประยุกต์ในการแปลงข้างต้นได้ถูกต้องเพียงใด? ฉันกล้ารับรองกับคุณว่าอันที่จริงการแปลงนั้นทำถูกต้องแล้ว การรู้เหตุผลทางคณิตศาสตร์ของเลขคณิต พีชคณิตบูลีน และส่วนอื่นๆ ของคณิตศาสตร์ก็เพียงพอแล้ว มันคืออะไร? คราวหน้าจะเล่าให้ฟังค่ะ

สำหรับ supersets เป็นไปได้ที่จะรวมสองชุดเป็น superset เดียวโดยการเลือกหน่วยการวัดที่มีอยู่ในองค์ประกอบของสองชุดนี้

อย่างที่คุณเห็น หน่วยวัดและคณิตศาสตร์ทั่วไปทำให้ทฤษฎีเซตกลายเป็นอดีตไปแล้ว สัญญาณที่บ่งบอกว่าทฤษฎีเซตไม่ดีนักก็คือนักคณิตศาสตร์ได้ใช้ภาษาและสัญกรณ์สำหรับทฤษฎีเซตขึ้นมาเอง นักคณิตศาสตร์ทำในสิ่งที่หมอผีเคยทำ หมอผีเท่านั้นที่รู้วิธี "ใช้" อย่าง "ถูกต้อง" อย่าง "ความรู้" "ความรู้" นี้สอนเรา

สุดท้ายนี้ ฉันต้องการแสดงให้คุณเห็นว่านักคณิตศาสตร์จัดการอย่างไร

วันจันทร์ที่ 7 มกราคม 2019

ในศตวรรษที่ 5 ก่อนคริสต์ศักราช นักปรัชญาชาวกรีกชื่อ Zeno แห่ง Elea ได้คิดค้น aporias ที่มีชื่อเสียงของเขา ซึ่งมีชื่อเสียงมากที่สุดคือ aporia "Achilles and the Tortoise" นี่คือเสียง:

สมมติว่าอคิลลิสวิ่งเร็วกว่าเต่าสิบเท่าและอยู่ข้างหลังเต่าพันก้าว ในช่วงเวลาที่ Achilles วิ่งระยะทางนี้ เต่าคลานไปหนึ่งร้อยก้าวไปในทิศทางเดียวกัน เมื่ออคิลลิสวิ่งร้อยก้าว เต่าจะคลานไปอีกสิบก้าว เป็นต้น กระบวนการนี้จะดำเนินต่อไปอย่างไม่มีกำหนด Achilles จะไม่มีวันไล่ตามเต่า

เหตุผลนี้กลายเป็นเรื่องที่น่าตกใจสำหรับคนรุ่นหลังทั้งหมด อริสโตเติล, ไดโอจีเนส, คานท์, เฮเกล, กิลเบิร์ต... ทั้งหมดนี้ถือว่าไม่ทางใดก็ทางหนึ่ง ถือว่าอาพอเรียของซีโน ช็อกหนักมากจน" ... การอภิปรายยังคงดำเนินต่อไปในขณะนี้ ชุมชนวิทยาศาสตร์ยังไม่มีความคิดเห็นร่วมกันเกี่ยวกับสาระสำคัญของความขัดแย้ง ... การวิเคราะห์ทางคณิตศาสตร์ ทฤษฎีเซต วิธีการทางกายภาพและปรัชญาใหม่ ๆ มีส่วนร่วมในการศึกษาประเด็นนี้ ; ไม่มีใครกลายเป็นวิธีแก้ปัญหาที่เป็นที่ยอมรับในระดับสากล ..."[วิกิพีเดีย" Aporias ของ Zeno "] ทุกคนเข้าใจว่าพวกเขากำลังถูกหลอก แต่ไม่มีใครเข้าใจว่าการหลอกลวงคืออะไร

จากมุมมองของคณิตศาสตร์ Zeno ใน aporia ของเขาแสดงให้เห็นอย่างชัดเจนถึงการเปลี่ยนแปลงจากค่าเป็น การเปลี่ยนแปลงนี้หมายถึงการใช้แทนค่าคงที่ เท่าที่ฉันเข้าใจ เครื่องมือทางคณิตศาสตร์สำหรับการใช้หน่วยการวัดแบบแปรผันยังไม่ได้รับการพัฒนา หรือยังไม่ได้นำไปใช้กับ aporia ของ Zeno การใช้ตรรกะปกติของเรานำเราไปสู่กับดัก โดยความเฉื่อยของการคิด เราใช้หน่วยเวลาคงที่กับส่วนกลับกัน จากมุมมองทางกายภาพ ดูเหมือนว่าจะช้าลงจนกระทั่งหยุดโดยสมบูรณ์ในขณะที่ Achilles ไล่ตามเต่า หากเวลาหยุดลง Achilles จะไม่สามารถแซงเต่าได้อีกต่อไป

ถ้าเราเปลี่ยนตรรกะที่เราคุ้นเคย ทุกอย่างก็เข้าที่ Achilles วิ่งด้วยความเร็วคงที่ เส้นทางที่ตามมาแต่ละส่วนจะสั้นกว่าส่วนก่อนหน้าสิบเท่า ดังนั้นเวลาที่ใช้ในการเอาชนะมันจึงน้อยกว่าครั้งก่อนถึงสิบเท่า หากเราใช้แนวคิดเรื่อง "อินฟินิตี้" ในสถานการณ์นี้ ก็คงถูกต้องที่จะบอกว่า "อคิลลิสจะแซงเต่าอย่างรวดเร็วอย่างไม่สิ้นสุด"

จะหลีกเลี่ยงกับดักตรรกะนี้ได้อย่างไร? คงอยู่ในหน่วยของเวลาคงที่และอย่าเปลี่ยนเป็นค่าส่วนกลับ ในภาษาของ Zeno มีลักษณะดังนี้:

ในช่วงเวลาที่อคิลลิสวิ่งพันก้าว เต่าคลานไปหนึ่งร้อยก้าวไปในทิศทางเดียวกัน ในช่วงเวลาถัดไป เท่ากับครั้งแรก จุดอ่อนจะวิ่งต่อไปอีกพันก้าว และเต่าจะคลานหนึ่งร้อยก้าว ตอนนี้ Achilles เร็วกว่าเต่าแปดร้อยก้าว

วิธีการนี้อธิบายความเป็นจริงได้อย่างเพียงพอโดยไม่มีข้อขัดแย้งเชิงตรรกะใดๆ แต่นี่ไม่ใช่วิธีแก้ปัญหาที่สมบูรณ์ คำกล่าวของไอน์สไตน์เกี่ยวกับความเร็วแสงที่ไม่อาจเทียบได้นั้นคล้ายกับคำว่าอคิลลีสกับเต่าของซีโนมาก เรายังไม่ได้ศึกษา คิดใหม่ และแก้ปัญหานี้ และจะต้องไม่ค้นหาวิธีแก้ปัญหาในจำนวนมาก แต่ในหน่วยการวัด

aporia ที่น่าสนใจอีกอย่างของ Zeno เล่าถึงลูกศรที่บินได้:

ลูกศรที่บินได้นั้นไม่มีการเคลื่อนไหว เนื่องจากมันหยุดนิ่งทุกขณะ และเนื่องจากมันหยุดนิ่งอยู่ทุกขณะ มันจึงหยุดนิ่งเสมอ

ใน aporia นี้ ความขัดแย้งเชิงตรรกะถูกเอาชนะอย่างง่ายดาย - เพียงพอที่จะชี้แจงว่าในแต่ละช่วงเวลาลูกศรที่บินได้หยุดนิ่งอยู่ที่จุดต่าง ๆ ในอวกาศซึ่งอันที่จริงแล้วเป็นการเคลื่อนไหว มีจุดอื่นที่จะสังเกตที่นี่ จากภาพถ่ายรถหนึ่งภาพบนท้องถนน เป็นไปไม่ได้ที่จะระบุข้อเท็จจริงของการเคลื่อนที่หรือระยะห่างของรถคันดังกล่าว ในการพิจารณาข้อเท็จจริงของการเคลื่อนที่ของรถ จำเป็นต้องใช้ภาพถ่ายสองภาพที่ถ่ายจากจุดเดียวกัน ณ จุดต่างๆ ในเวลาที่ต่างกัน แต่ไม่สามารถใช้เพื่อกำหนดระยะทางได้ ในการกำหนดระยะห่างจากรถ คุณต้องมีรูปถ่ายสองภาพที่ถ่ายจากจุดต่างๆ ในอวกาศในเวลาเดียวกัน แต่คุณไม่สามารถระบุข้อเท็จจริงของการเคลื่อนที่จากจุดเหล่านั้นได้ (โดยปกติ คุณยังต้องการข้อมูลเพิ่มเติมสำหรับการคำนวณ ตรีโกณมิติจะช่วยคุณได้) สิ่งที่ฉันต้องการจะชี้ให้เห็นโดยเฉพาะคือจุดสองจุดในเวลาและจุดสองจุดในอวกาศเป็นสองสิ่งที่แตกต่างกันซึ่งไม่ควรสับสนเนื่องจากให้โอกาสในการสำรวจที่แตกต่างกัน
ฉันจะแสดงกระบวนการพร้อมตัวอย่าง เราเลือก "ของแข็งสีแดงในสิว" - นี่คือ "ทั้งหมด" ของเรา ในเวลาเดียวกันเราจะเห็นว่าสิ่งเหล่านี้มีคันธนูและไม่มีคันธนู หลังจากนั้นเราเลือกส่วนหนึ่งของ "ทั้งหมด" และสร้างชุด "ด้วยธนู" นี่คือวิธีที่หมอดูเลี้ยงตัวเองโดยเชื่อมโยงทฤษฎีเซตกับความเป็นจริง

ตอนนี้มาทำเคล็ดลับเล็กน้อย ลองใช้ "ก้อนสิวด้วยธนู" และรวม "ทั้งหมด" เหล่านี้ด้วยสีโดยเลือกองค์ประกอบสีแดง เรามี "สีแดง" มากมาย ตอนนี้เป็นคำถามที่ยาก: ชุดที่ได้รับ "พร้อมคันธนู" และ "สีแดง" เป็นชุดเดียวกันหรือสองชุดต่างกันหรือไม่ หมอผีเท่านั้นที่รู้คำตอบ แม่นยำยิ่งขึ้นพวกเขาเองไม่รู้อะไรเลย แต่อย่างที่พวกเขาพูดก็เป็นเช่นนั้น

ตัวอย่างง่ายๆ นี้แสดงให้เห็นว่าทฤษฎีเซตนั้นไร้ประโยชน์อย่างสิ้นเชิงเมื่อพูดถึงความเป็นจริง ความลับคืออะไร? เราสร้างชุด "สิวสีแดงที่มีธนู" การก่อตัวเกิดขึ้นตามหน่วยการวัดที่แตกต่างกันสี่หน่วย: สี (สีแดง), ความแข็งแรง (ของแข็ง), ความหยาบ (เป็นรอย), ของประดับตกแต่ง (ด้วยธนู) มีเพียงชุดของหน่วยวัดเท่านั้นที่ทำให้สามารถอธิบายวัตถุจริงในภาษาของคณิตศาสตร์ได้อย่างเพียงพอ. นี่คือสิ่งที่ดูเหมือน

ตัวอักษร "a" ที่มีดัชนีต่างกันหมายถึงหน่วยวัดที่ต่างกัน ในวงเล็บ จะเน้นหน่วยของการวัดตามที่มีการจัดสรร "ทั้งหมด" ในขั้นตอนเบื้องต้น หน่วยวัดตามที่ตั้งชุดนั้นถูกนำออกจากวงเล็บ บรรทัดสุดท้ายแสดงผลสุดท้าย - องค์ประกอบของชุด อย่างที่คุณเห็น หากเราใช้หน่วยเพื่อสร้างเซต ผลลัพธ์จะไม่ขึ้นอยู่กับลำดับการกระทำของเรา และนี่คือคณิตศาสตร์ ไม่ใช่การเต้นรำของหมอผีกับรำมะนา หมอผีสามารถ "ใช้สัญชาตญาณ" เพื่อให้ได้ผลลัพธ์แบบเดียวกัน โดยโต้แย้งด้วย "ความชัดเจน" เนื่องจากหน่วยการวัดไม่รวมอยู่ในคลังแสง "ทางวิทยาศาสตร์" ของพวกเขา

ด้วยความช่วยเหลือของหน่วยการวัด มันง่ายมากที่จะแยกหนึ่งชุดหรือรวมหลายชุดเป็นซุปเปอร์เซ็ตเดียว มาดูพีชคณิตของกระบวนการนี้กันดีกว่า